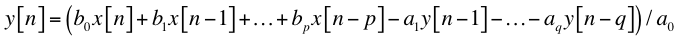
This page presents a major revision to my S-Domain Bode/Nyquist Plot Java applet, offering all of the same features but now in the Z-domain. As in the S-Domain version the focus remains on design of cascaded filter sections, so numerator and denominator are still entered as one or more polynomials, which get multiplied and terms collected before plotting. While I've enjoyed writing Java applets as a hobby for almost 15 years, security restrictions have increased to the point where they are no longer useful. Even if you can get over the hurdles placed in your way by software publishers, there is still the issue that applets no longer interact with the system clipboard, so now you have to type in all the filter coefficients by hand. You can always download my jar file or build the applet yourself from source. The Eclipse IDE is especially convenient for this. Most of you will see screen shots of the applet on this page, replacing the real thing when Java is disabled.
Digital filters meant to operate in real time depend on current and previous inputs x as a time series (FIR and IIR filters), and on previous outputs y as a time series (IIR filters ony). As shown in the difference equation, filter coefficients bi act on the input series x, while filter coefficients aj act on the output series y.
The difference equation can be transformed into a transfer function H(z) where the numerator is a polynomial in z representing the input time series, and the denominator is a polynomial in z representing the output time series. Here, z represents the unit time delay of one sample interval. It is convenient to assume uniform time intervals between samples, but not required for this derivation.
Bode and Nyquist plots of the steady state amplitude and phase response of the digital filter are obtained by replacing z with ejω, where j is the square root of -1 and ω is the angular frequency of the input in units of radians/sample. Now I'll derive some common filter types with the simplification that roots of the denominator (poles of the transfer function) all lie on the real axis.
The simplest transfer function in the z domain which we'll consider here is the first order low-pass filter. There is only one tunable parameter α which appears in the numerator to set the gain equal to unity far below the cutoff frequency, and in the denominator to set the cutoff frequency.
We can improve performance a bit by taking input from both the current sample and the previous sample, each weighted by a factor of 1/2. The parameter α can be found by setting the transfer function equal to (0.5 - 0.5j) and solving for α in terms of z, where z has been replaced with ejω.
The following examples have been tuned to a corner frequency of 1 kHz, with a sample rate of 44100 samples/second. Values which depend on α are given in the following table.
| Description | Value |
|---|---|
| Sample Rate | 44100 samples/second |
| Corner Frequency | 1 kHz = 0.142476 radians/sample |
| α | 0.86678843 |
| α2 | 0.75132218 |
| 2α | 1.73357686 |
| 4α | 3.46715372 |
A second order low-pass filter is formed by linking two first order low-pass filters in series. The transfer functions are multiplied, resulting in a response of (0 - 0.5j) at the corner frequency.
Just as in the S-domain, Z-domain coefficients are expressed from left to right in decreasing order. The difference is that in the Z-domain we start with constant terms (zeroth order) on the left, and proceed towards more negative terms on the right. For this reason, zero-valued coefficients on the right are optional in Z-domain polynomials, but those on the left are not, just the opposite of the S-domain case.
A first order high-pass filter is formed by subtracting the first order low-pass filter from unity. This gives a reponse of (0.5 + 0.5j) at the corner frequency.
A second order high-pass filter is then formed by linking two first order high-pass filters in series. The transfer functions are multiplied, resulting in a response of (0 + 0.5j) at the corner frequency.
Amplitude is plotted in blue, while phase is plotted in magenta. If you try to plot frequencies above the Nyquist limit, which is half the sampling rate, the plot will appear in gray.
A band-pass filter is formed by linking a low-pass filter and a high-pass filter in series. The transfer functions are multiplied, resulting in a response of (0.5 + 0j) at the corner frequency.
A first order all-pass filter is formed by taking the difference between a first order high-pass filter and a first order low-pass filter. The resulting filter can be made second order by linking two of them in series. The transfer function is squared, making the filter second order and resulting in a response of (-1 + 0j) at the corner frequency.
A notch filter is formed by taking the average of a second order all-pass filter and unity. This results in a response of (0 + 0j) at the corner frequency.
The transfer functions shown so far all implement IIR (Infinite Impulse Response) filters, because they depend on both the input series and the output series. But the BodeZ applet presented here also works nicely with FIR (Finite Impulse Response) filters, which depend only on the input series. Leave the denominator field blank, and the a0 coefficient will default to unity. Or place a constant value in the denominator field (as shown below) to normalize the gain. An interesting example of an FIR filter is the running average, which gives a series of harmonically related notches in its amplitude response. The filter shown here has notches at one-eighth of the sample rate (5512.5 Hz), one-fourth the sample rate (11025 Hz), three-eighths the sample rate (16537.5 Hz), and one-half the sample rate (22050 Hz).
If running this applet on-line you'll have to type all the filter coefficients by hand, which can be a lot of work. If running off-line however, you can just copy-and-paste the impulse response of any filter you find interesting, even with hundreds of coefficients. You can obtain the impulse response from an s-domain transfer function by using my S-Domain Bode Plot applet, and then past it into the Z-Domain Bode Plot applet presented here to quickly design an FIR filter. I use Excel to pull out the impulse response from the table data. You'll probably want to truncate the impulse response series at some point, to minimize artifacts in the response.
At some point in the future I'll post a Python script here, which verifies the output from this applet. In the mean time, feel free to try out any text-book or real-world transfer functions you find interesting. If you find any anomalies or pathologies, please let me know at the email address given in the graphic at the bottom of this page.
I am placing the ideas and source code presented on this page in the public domain, for the benefit of software developers and engineers. Please remember that only you can determine if these ideas are suitable for your application. The burden is on you to verify, through functional test, code inspection, and any other means you determine is appropriate, whether the source code presented here actually works or not. And only you know if you are qualified to make modifications to the source code presented here. Feel free to post a link to this page on your site, but please don't copy my content. This page should be available at this URL for the foreseeable future. I claim a trademark interest in the names "Williamsonic" and "www.williamsonic.com".